Archive for the ‘History’ Category

Page 8 of 16

East of my day's circle

Published by peter on 2011-07-28 in Heroes, History, Literature, Religion and Shakespeare. 0 Comments

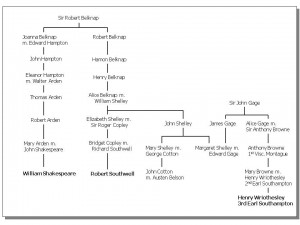
I have written before about Robert Southwell SJ, poet, martyr and Shakespeare’s cousin, and quoted some of his poems.  Southwell (c. 1561-1595) was an English Jesuit from an aristocratic family, whose mother had been a governess and friend of Queen Elizabeth I.  He left England illegally to study for the priesthood and returned — again illegally — to live and minister in secret to England’s oppressed Catholic population.  He was captured, tortured by Elizabeth’s sadistic religious police, subjected to a show trial, and publicly executed.
Southwell was a poet of fine sensitivity, and drew on his Jesuit spiritual training to become the first English poet to develop personation (or subjectivity), a psychologically-real description of the interior self.   His cousin Will Shakespeare was to adopt this idea in his poetry and plays, so that (for example) we learn about Hamlet’s internal mental deliberations, not only about his public actions and conversations.  The late Anne Sweeney argued that Southwell developed personation in his poetry as a direct result of completing the Spiritual Exercises of St. Ignatius Lopez of Loyala, a process of meditation and self-reflection which all Jesuits undertake. In her words (p. 80):

The core experience of the Ignatian Exercises was the reading and learning of the hidden self, the exercisant learning to define his reponses according to a Christian morality that would then moderate his behaviour. After a powerfully imagined involvement in, say, Christ’s birth, he was required to withdraw the mind’s eye from the scene before him and redirect it into himself to analyse with care the feelings thereby aroused.”

It would be interesting to know if Ignatius himself drew on literary models from (eg) Basque, Catalan or Spanish in devising the Exercises.

Living underground and on the run, Southwell wrote poetry for a community unable to obtain prayer books or to easily hear preachers;  poetry was thus a substitute for sermons and for personal spiritual counselling, and a form of prayer and spiritual meditation.  His poetry is also strongly visual.
Because the Jesuit mission to England during Elizabeth’s reign was forced underground it is not surprising that Jesuit priests mostly lived in the homes of rich or noble Catholics, or Catholic sympathizers, sometimes hidden in secret chambers.    It is more surprising that there were still English nobles willing to risk everything (their wealth, their titles, their freedom, their homeland, their lives) to hide these priests.   One such family was that of Philip Howard, the 20th Earl of Arundel (1557-1595), who was 10 years a prisoner of Elizabeth I, refusing to recant Catholicism, and who died in prison without ever meeting his own son.   Howard’s wife, Anne Dacre (1557-1630), was also a staunch Catholic.  The earldom of Arundel is the oldest extant earldom in the English peerage, dating from 1138.
The Howard’s London house on the Thames was one of the noble houses which sheltered Robert Southwell for several years.    The location of their home, between the present-day Australian High Commission and Temple Tube station,  is commemorated in the names of streets and buildings in the area:  Arundel Street, Surrey Street, Maltravers Street (all names associated with the Arundel family), Arundel House, Arundel Great Court Building, the former Swissotel Howard Hotel, and the former Norfolk Hotel (now the Norfolk Building in King’s College London) in Surrey Street.    Maltravers Street is currently the location for a nightly mobile soup kitchen.   Of course, in Elizabethan times the Thames was wider here, the Embankment only being built in the 19th century.   One can still find steps in some of the side streets leading to the Thames descending at the edge where the previous riverbank used to be, for instance on Milford Lane.
Southwell also, it seems, spent time in the London house of his cousin Henry Wriothesley, 3rd Earl of Southampton (1573-1624), who was also Shakespeare’s patron and cousin.    Southampton’s house then was a short walk away, in modern-day Chancery Lane, on the east side of Lincoln’s Inn fields.   Southampton was part of the rebellion of Robert Deveraux, 2nd Earl of Essex (1565-1601) against Elizabeth in February 1601. The London house of Essex was also along the Thames, downstream and adjacent to that of the Howard family.  The street names there also recall this history:  Essex Street, Devereaux Court.
Supporters of Essex, chiefly brothers of Henry Percy, 9th Earl of Northumberland (1564-1632), paid for a performance of Shakespeare’s play, Richard II, the evening before the rebellion.   Percy was married to Dorothy Devereaux (1564-1619), sister of Robert, and was regarded as a Catholic sympathizer.  Percy also employed Thomas Harriott (1560-1621), a member of the matherati. Given the physical proximity of these noble villas, it is likely too that Southwell and Harriott met and knew each other.
And, weirdly, Essex and Norfolk are adjacent streets in the Lower East Side of Manhattan, too (close by and parallel to Orchard Street).
References:
The image is Shown a plan of Arundel House, the London home of the Earls of Arundel, as it was in 1792 (from the British Library).  The church shown in the upper right corner is St. Clement Danes, now the home church of the Royal Air Force.
Christopher Devlin [1956]: The Life of Robert Southwell: Poet and Martyr.  New York, NY, USA:  Farrar, Straus and Cudahy.
Robert Southwell [2007]:  Collected Poems. Edited by Peter Davidson and Anne Sweeney.  Manchester, UK:  Fyfield Books.
Anne R. Sweeney [2006]: Robert Southwell: Snow in Arcadia:  Redrawing the English Lyric Landscape 1586-1595. Manchester, UK:  Manchester University Press.

Shakespeare's cousins

Published by peter on 2011-07-17 in Heroes, History, Literature and Poetry. 0 Comments

I have remarked before that whoever wrote William Shakespeare’s plays and poetry was deeply familiar with the poetry and prose of Robert Southwell SJ, and had access to Southwell’s works in manuscript form.  We know this because most of Southwell’s output was only published after his execution in 1595, and Shakespeare’s poetry shows Southwell’s influence well before this date.

Shakespeare and Southwell were cousins, and both were also cousins to Henry Wriothesley, third Earl of Southampton, Shakespeare’s patron and the likely dedicatee of the Sonnets.  John Klause, in his fine book tracing the influence of Southwell’s writing on Shakespeare’s own words, includes a family tree showing the family connections between these three Elizabethans.  I reproduce some of the tree below, copied from page 40 of Klause’s book. Southwell’s mother, Bridget Copley, was a governess to the young Princess Elizabeth, so the connections to the royal family were close. In addition, Southwell and Shakespeare were also connected through the Vaux and Throckmorton families (Devlin has another family tree, page 264).  

And the family connection between Southwell and Wriothesley was in fact closer than Klause’s tree indicates. Southwell’s eldest brother Richard married Alice Cornwallis, a niece of Henry Wriothesley senior, second Earl of Southampton and the third Earl’s father, and Southwell’s eldest sister Elizabeth married a nephew of the same second earl, a son of Margaret Wriothesley and Michael Lister.  Thus, Robert Southwell was twice a second cousin by marriage to Henry Wriothesley junior, third Earl (Devlin tree, p. 15).

References:
Christopher Devlin [1956]: The Life of Robert Southwell: Poet and Martyr.  New York, NY, USA:  Farrar, Straus and Cudahy.
John Klause [2008]: Shakespeare, the Earl, and the Jesuit. Teaneck, NJ, USA: Fairleigh Dickinson University Press.

Oral culture

Published by peter on 2011-06-11 in Argumentation, History, Politics and Rhetoric. 0 Comments

For about the last 300 years, and especially from the introduction of universal public education in the late 19th century, western culture has  been dominated by text and writing.  Elizabethan culture, by contrast, was primarily oral:  Shakespeare, for example, wrote his plays to be performed not to be read, and did not even bother to arrange definitive versions for printing.  

One instance of the culture-wide turn from speech to text was a switch from spoken to written mathematics tests in the west which occurred at Cambridge in the late 18th century, as I discuss here.  There is nothing intrinsically better about written examinations over spoken ones, especially when standardized and not tailored for each particular student.  This is true even for mathematics, as is shown by the fact that oral exams are still the norm in university mathematics courses in the Russian-speaking world; Russia continues to produce outstanding mathematicians.

Adventurer and writer Rory Stewart, now an MP,  has an interesting post about the oral culture of the British Houses of Parliament, perhaps the last strong-hold of argument-through-speech in public culture.  The only other places in modern life, a place which is not quite as public, where speech reigns supreme, are court rooms.

Patrick Leigh Fermor RIP

Published by peter on 2011-06-11 in Classics, Heroes, History, Obituaries and Poetry. 0 Comments

The Grauniad reports on the death of adventurer  and writer Patrick Leigh Fermor, aged 96.  I recount a story about him and an ode by Horace, here.

Fermor attended Kit Marlowe’s old school, King’s School Canterbury, together with Alan Watts, who apparently wrote his first book about Zen Buddhism while still at school.   Fermor famously was expelled from this school.
 

Australian improv comedy pre-history

Published by peter on 2011-05-28 in Creativity, History and Matherati. 0 Comments

My father saw a young Melbourne comedian named Barry Humphries try out an act as an ordinary Moonee Ponds housewife in a Review at the Phillip Street Theatre in Sydney in about 1955.   He and I saw undergraduate mathematician Adam Spencer winning theatre sports improv contests at The Harold Park Hotel in about 1988.   As well as being so witty that I would remember his name all this time, he also still had a full head of blonde hair.

Let Newton Be!

Published by peter on 2011-04-20 in History, Matherati, Religion, Science and Theatre and Drama. 0 Comments

Belately, I want to record a play seen at the headquarters of The Royal Society in London last month, Let Newton Be, written by Craig Baxter, but using only Isaac Newton’s own words.     The play was interesting although the energy of the play sagged at times, particularly in the first half.   The story only barely mentioned Newton’s interest in alchemy, and seemed to overlook his brutal, deadly campaigns against money forgers later in life (or did I nap through that scene?)
The play comprised three actors, two men and a woman, who played Newton at different ages – as a child, as a young-ish Cambridge academic, and as an old man.  As a work of drama, the conceit worked well, although it was best when one of the actors was playing another person interacting with Newton (eg, Halley, and later Leibniz, who spoke in an amusing cod-German accent).  Perhaps the real Newton was not sufficiently schizoid for three actors to play him, at least not when constrained to only use the man’s written words.    As I have remarked before, Newton’s personality was all of a piece:  it is only modern westerners who cannot imagine a religious motivation for activities such as scientific research, for example, or who find alchemy and calculus incoherent.
The performance was followed by a panel discussion by the Great and the Good – two historians and two scientists.  One of the scientists was the Astronomer Royal, Sir Martin Rees, who has subsequently won this year’s Templeton Prize for Science and Religion.  The discussion was interesting, so it is a pity it was not recorded for posterity.
A review of another play about a member of the matherati, Kurt Godel, is here.

Antikythera

Published by peter on 2010-12-18 in Classics, Computer Science, Computer technology, Computing-as-interaction, History, Mathematics and Prophecy. 0 Comments

An orrery is a machine for predicting the movements of heavenly bodies.   The oldest known orrery is the Antikythera Mechanism, created in Greece around 2100 years ago, and rediscovered in 1901 in a shipwreck near the island of  Antikythera (hence its name).   The high-quality and precision nature of its components would indicate that this device was not unique, since the making of high-quality mechanical components is not trivial, and is not usually achieved with just one attempt (something Charles Babbage found, and which delayed his development of computing machinery immensely).
It took until 2006 and the development of x-ray tomography for a plausible theory of the purpose and operations of the Antikythera Mechanism to be proposed (Freeth et al. 2006).   The machine was said to be a physical examplification of  late Greek theories of cosmology, in particular the idea that the motion of a heavenly body could  be modeled by an epicycle – ie, a body traveling around a circle, which is itself moving around some second circle.  This model provided an explanation for the fact that many heavenly bodies appear to move at different speeds at different times of the year, and sometimes even (appear to) move backwards.
There have been two recent developments:  One is the re-creation of the machine (or, rather, an interpretation of it)  using lego components.
The second has arisen from a more careful examination of the details of the mechanism.  According to Marchant (2010), some people now believe that the mechanism examplifies Babylonian, rather than Greek, cosmology.   Babylonian astronomers modeled the movements of heavenly bodies by assuming each body traveled along just one circle, but at two different speeds:  movement in one period of the year being faster than during the other part of the year.
If this second interpretation of the Antikythera Mechanism is correct, then perhaps it was the mechanism itself (or others like it) which gave late Greek astronomers the idea for an epicycle model.   In support of this view is the fact that, apparently, gearing mechanisms and the epicycle model both appeared around the same time, with gears perhaps a little earlier.   So late Greek cosmology (and perhaps late geometry) may have arisen in response to, or at least alongside, practical developments and physical models.   New ideas in computing typically follow the same trajectory – first they exist in real, human-engineered, systems; then, we develop a formal, mathematical theory of them.   Programmable machines, for instance, were invented in the textile industry in the first decade of the 19th century (eg, the Jacquard Loom), but a mathematical theory of programming did not appear until the 1960s.   Likewise, we have had a fully-functioning, scalable, global network enabling multiple, asynchronous, parallel, sequential and interleaved interactions since Arpanet four decades ago, but we still lack a thorough mathematical theory of interaction.
And what have the Babylonians ever done for us?   Apart from giving us our units for measuring of time (divided into 60) and of angles (into 360 degrees)?
References:
T Freeth, Y Bitsakis, X Moussas, JH Seiradaki, A Tselikas, H Mangou, M Zafeiropoulou, R Hadland, D Bate, A Ramsey, M Allen, A Crawley, P Hockley, T Malzbender, D Gelb,W Ambrisco and MG Edmunds [2006]:  Decoding the ancient Greek astronomical calculator known as the Antikythera Mechanism.  Nature,  444 (30):   587-591.  30 November 2006.
J. Marchant [2010]:  Mechanical inspiration.  Nature, 468:  496-498.  25 November 2010.

Bob's your uncle

Published by peter on 2010-12-17 in Africa and History. 0 Comments

Being a colleague of Robert Mugabe greatly increases your chances of an early death, especially in a car accident.      Here’s a list of people who met unexpected ends while working with Bob (showing the year of their death).  No doubt the car accidents are due to chance.

  • Herbert Chitepo (1975), ZANU leader, killed by car bomb in exile in Lusaka.
  • Josiah Tongogara (1979), ZANLA leader, died in a car accident in Mozambique during return from exile.
  • Charles Tazvishaya (aka Lovemore Mawisa) (1986), personal private secretary to Prime Minister Mugabe, survived a gunshot wound to the head inflicted in the bedroom of his house and then died in Parirenyatwa Hospital, Harare, a fortnight later, after his medical drip was detached from the source medication.
  • Maurice Nyagumbo (1989), Minister for Mines, died from ingesting pesticide.
  • Border Gezi (2001), Minister for Gender, Youth and Employment, died in a car accident.
  • Moven Mahachi (2001), Minister of Defence, died in a car accident.
  • Elliot Manyika (2008), Minister Without Portfolio and National Political Commissar for ZANU-PF, died  in a car accident.
  • Susan Tsvangirai (2009), wife of Morgan Tsvangirai, the new Prime Minister in the Government of National Unity, died in a car accident.
  • General Solomon Mujuru (aka Rex Nhongo) (August 2011), former Commander-in-Chief of the Zimbabwe Armed Forces and husband of Vice President Joice Mujuru, died in a house fire which destroyed his farmhouse near Beatrice.

At the going down of the sun, and in the morning

Published by peter on 2010-11-07 in Heroes, History and Obituaries. 0 Comments

Anti-tank-trap-PaddysFlat
Non-Australians are often unaware how fearful Australians were of being invaded by Japanese Imperial Forces during World War II.  Australians had good reason to be fearful, since Japanese aircraft ran nearly 100 bombing raids on northern Australian towns and settlements, Japanese submarines planted mines in Sydney Harbour, submarines launched bombardments on both Sydney and Newcastle, and they harassed East Coast merchant shipping.  The Japanese regime even printed special banknotes for use as currency in an occupied Australia.   As a result, preparing for an invasion, Australian home forces were deployed, among other activities, in building tank traps – concrete pyramids intended to impede the advance of any invading tanks – on the main roads as far south as northern New South Wales (some 1500 miles down the east coast).  The photo above shows an anti-tank trap at Paddy’s Flat near Jenny Lind Creek, Tabulam, northern NSW. A key election issue in the 1943 Federal Election was whether the Opposition parties, when previously in Government at the start of the war, had approved a plan to abandon the entire north of Australia above Brisbane to the invaders.
Several members of my family fought to defend Australia and the region from Japanese imperialism and fascism, and some died in that defence.    Growing up with relatives, family friends, and acquaintances who’d been prisoners of war of the Japanese military perhaps gives one an acute sense of the myriad war crimes committed by those forces during that war, and of the many longer-term physical and psychological consequences of those crimes.  Unlike former POWs of the Wehrmacht, most former POWs of the Japanese military refused to speak of their prison-camp experiences, so horrific and unspeakable were they, and many survivors found themselves unable to cope with everyday life when the war ended.
In the week of Remembrance Day, I wanted to honour those members of my family who fell fighting in that war, or afterwards from its traumas:
Con Hanley (1885-1944), Charles B. McBurney (1890-1943), Cecil C. Sexton (1915-1942), and Ron M. Hanley (1918-1946).

Hardy on the Tripos

Published by peter on 2010-11-01 in History, Mathematics and Matherati. 0 Comments


Lest anyone think I’m uniquely deranged for my criticisms of the Cambridge University Mathematics Tripos examination, particularly during the 18th- and 19th-centuries, here is GH Hardy – perhaps Britain’s greatest 20th century pure mathematician – speaking in his Presidential Address to the Mathematics Association in 1926:

My own contribution to the discussion consisted merely in an expression of my feeling that the best thing that could happen to English mathematics, and to Cambridge mathematics in particular, would be that the Mathematical Tripos should be abolished. I stated this on the spur of the moment, but it is my considered opinion, and I propose to defend it at length to-day. And I am particularly anxious that you should understand quite clearly that I mean exactly what I say; that by “abolished” I mean “abolished”, and not “reformed”; that if I were prepared to co-operate, as in fact I have co-operated in the past, in “reforming” the Tripos, it would be because I could see no chance of any more revolutionary change; and that my “reforms” would be directed deliberately towards destroying the traditions of the examination and so preparing the way for its extinction.” [p. 134]
. . .
“I suppose that it would be generally agreed that Cambridge mathematics, during the last hundred years, has been dominated by the Mathematical Tripos in a way in which no first-rate subject in any other first-rate university [page-break] has ever been dominated by an examination. It would be easy for me, were the fact disputed, to justify my assertion by a detailed account of the history of the Tripos, but this is unnecessary, since you can find an excellent account, written by a man who was very much more in sympathy with the Tripos than I am, in Mr. Rouse Ball’s History of Mathematics in Cambridge. I must, however, call your attention to certain rather melancholy reflections which the history of Cambridge mathematics suggests. You will understand that when I speak of mathematics I mean primarily pure mathematics, not that I think that anything which I say about pure mathematics is not to a great extent true of applied mathematics also, but merely because I do not want to criticise where my competence as a critic is doubtful.
Mathematics at Cambridge challenges criticism by the highest standards. England is a first-rate country, and there is no particular reason for supposing that the English have less natural talent for mathematics than any other race; and if there is any first-rate mathematics in England, it is in Cambridge that it may be expected to be found. We are therefore entitled to judge Cambridge mathematics by the standards that would be appropriate in Paris or Gottingen or Berlin. If we apply these standards, what are the results?  I will state them, not perhaps exactly as they would have occurred to me spontaneously – though the verdict is one which, in its essentials, I find myself unable to dispute – but as they were stated to me by an outspoken foreign friend.
In the first place, about Newton there is no question; it is granted that he stands with Archimedes or with Gauss. Since Newton, England has produced no mathematician of the very highest rank. There have been English mathematicians, for example Cayley, who stood well in the front rank of the mathematicians of their time, but their number has been quite extraordinarily small; where France or Germany produces twenty or thirty, England produces two or three. There has been no country, of first-rate status and high intellectual tradition, whose standard has been so low; and no first-rate subject, except music, in which England has occupied so consistently humiliating a position. And what have been the peculiar characteristics of such English mathematics as there has been? Occasional flashes of insight, isolated achievements sufficient to show that the ability is really there, but, for the most part, amateurism, ignorance, incompetence, and triviality. It is indeed a rather cruel judgment, but it is one which any competent critic, surveying the evidence dispassionately, will find it uncommonly difficult to dispute.
I hope that you will understand that I do not necessarily endorse my friend’s judgment in every particular. He was a mathematician whose competence nobody could question, and whom nobody could accuse of any prejudice against England, Englishmen, or English mathematicians; but he was also, of course, a man developing a thesis, and he may have exaggerated a little in the enthusiasm of the moment or from curiosity to see how I should reply.  Let us assume that it is an exaggerated judgment, or one rhetorically expressed.  It is, at any rate, not a ridiculous judgment, and it is serious enough that such a condemnation, from any competent critic, should not be ridiculous. It is inevitable that we should ask whether, if such a judgment can really embody any sort of approximation to the truth, some share of the responsibility must not be laid on the Mathematical Tripos and the grip which it has admittedly exerted on English mathematics.
I am anxious not to fall into exaggeration in my turn and use extravagant language about the damage which the Tripos may have done, and it would no doubt be an extravagance to suggest that the most ruthless of examinations could destroy a whole side of the intellectual life of a nation. On the [page-break] other hand it is really rather difficult to exaggerate the hold which the Tripos has exercised on Cambridge mathematical life, and the most cursory survey of the history of Cambridge mathematics makes one thing quite clear; the reputation of the Tripos, and the reputation of Cambridge mathematics stand in correlation with one another, and the correlation is large and negative.  As one has developed, so has the other declined. As, through the early and middle nineteenth century, the traditions of the Tripos strengthened, and its importance in the eyes of the public grew greater and greater, so did the external reputation of Cambridge as a centre of mathematical learning steadily decay. When, in the years perhaps between 1880 and 1890, the Tripos stood, in difficulty, complexity, and notoriety, at the zenith of its reputation, English mathematics was somewhere near its lowest ebb. If, during the last forty years, there has been an obvious revival, the fortunes of the Tripos have experienced an equally obvious decline.” [pp. 135-137]
. . .
“It has often been said that Tripos mathematics was a collection of elaborate futilities, and the accusation is broadly true. My own opinion is that this is the inevitable result, in a mathematical examination, of high standards and traditions. The examiner is not allowed to content himself with testing the competence and the knowledge of the candidates; his instructions are to provide a test of more than that, of initiative, imagination, and even of some sort of originality. And as there is only one test of originality in mathematics, namely the accomplishment of original work, and as it is useless to ask a youth of twenty-two to perform original research under examination conditions, the examination necessarily degenerates into a kind of game, and instruction for it into initiation into a series of stunts and tricks. It was in any case certainly true, at the time of which I am speaking, that an undergraduate might study mathematics diligently throughout the whole of his career, and attain the very highest honours in the examination, without having acquired, and indeed without having encountered, any knowledge at all of any of the ideas which dominate modern mathematical thought. His ignorance of analysis would have been practically complete. About geometry I speak with less confidence, but I am sure that such knowledge as he possessed would have been exceedingly one-sided, and that there would have been whole fields of geometrical knowledge, and those perhaps the most fruitful and fascinating of all, of which he would have known absolutely nothing. A mathematical physicist, I may be told, would on the contrary have received an appropriate and an excellent education. It is possible; it would no doubt be very impertinent for me to deny it. Yet I do remember Mr. Bertrand Russell telling me that he studied electricity at Trinity for three years, and that at the end of them he had never heard of Maxwell’s equations; and I have also been told by friends whom I believe to be competent that Maxwell’s equations are really rather important in physics. And when I think of this I begin to wonder whether the teaching of applied mathematics was really quite so perfect as I have sometimes been led to suppose.” [p. 138]
. . .
“I shall judge the Tripos by its real or apparent influence on English mathematics. I have already told you that in my judgment this influence has in the past been bad, that the Tripos has done negligible good and by no means negligible harm, and that, so far from being the great glory of Cambridge mathematics, it has gone a very long way towards strangling its development.”  [p. 141]

 
Reference:
G. H. Hardy [1926/1948]: Presidential Address: The Case against the Mathematical Tripos. The Mathematical Gazette, 32 (300): 134-145 (July 1948).