With the history and pioneers of computing in the British news this week, I’ve been thinking about a common misconception: many people regard computer science as very closely related to Mathematics, perhaps even a sub-branch of Mathematics. Mathematicians and physical scientists, who often know little and that little often outdated about modern computer science and software engineering, are among the worst offenders here. For some reason, they often think that computer science consists of Fortran programming and the study of algorithms, which has been a long way from the truth for, oh, the last few decades. (I have past personal experience of the online vitriol which ignorant pure mathematicians can unleash on those who dare to suggest that computer science might involve the application of ideas from philosophy, economics, sociology or ecology.)
So here’s my story: Computer Science is the love-child of Pure Mathematics and Philosophy.
Continue reading ‘Computer Science, love-child’
Archive for the ‘Mathematics’ Category
Page 8 of 9
Alan Turing
Yesterday, I reported on the restoration of the world’s oldest, still-working modern computer. Last night, British Prime Minister Gordon Brown apologized for the country’s treatment of Alan Turing, computer pioneer. In the words of Brown’s statement:
Turing was a quite brilliant mathematician, most famous for his work on breaking the German Enigma codes. It is no exaggeration to say that, without his outstanding contribution, the history of World War Two could well have been very different. He truly was one of those individuals we can point to whose unique contribution helped to turn the tide of war. The debt of gratitude he is owed makes it all the more horrifying, therefore, that he was treated so inhumanely. In 1952, he was convicted of ‘gross indecency’ – in effect, tried for being gay. His sentence – and he was faced with the miserable choice of this or prison – was chemical castration by a series of injections of female hormones. He took his own life just two years later.”
It might be considered that this apology required no courage of Brown.
This is not the case. Until very recently, and perhaps still today, there were people who disparaged and belittled Turing’s contribution to computer science and computer engineering. The conventional academic wisdom is that he was only good at the abstract theory and at the formal mathematizing (as in his “schoolboy essay” proposing a test to distinguish human from machine interlocuters), and not good for anything practical. This belief is false. As the philosopher and historian B. Jack Copeland has shown, Turing was actively and intimately involved in the design and construction work (mechanical & electrical) of creating the machines developed at Bletchley Park during WWII, the computing machines which enabled Britain to crack the communications codes used by the Germans.
Perhaps, like myself, you imagine this revision to conventional wisdom would be uncontroversial. Sadly, not. On 5 June 2004, I attended a symposium in Cottonopolis to commemorate the 50th anniversary of Turing’s death. At this symposium, Copeland played a recording of an oral-history interview with engineer Tom Kilburn (1921-2001), first head of the first Department of Computer Science in Britain (at the University of Manchester), and also one of the pioneers of modern computing. Kilburn and Turing had worked together in Manchester after WW II. The audience heard Kilburn stress to his interviewer that what he learnt from Turing about the design and creation of computers was all high-level (ie, abstract) and not very much, indeed only about 30 minutes worth of conversation. Copeland then produced evidence (from signing-in books) that Kilburn had attended a restricted, invitation-only, multi-week, full-time course on the design and engineering of computers which Turing had presented at the National Physical Laboratories shortly after the end of WW II, a course organized by the British Ministry of Defence to share some of the learnings of the Bletchley Park people in designing, building and operating computers. If Turing had so little of practical relevance to contribute to Kilburn’s work, why then, one wonders, would Kilburn have turned up each day to his course.
That these issues were still fresh in the minds of some people was shown by the Q&A session at the end of Copeland’s presentation. Several elderly members of the audience, clearly supporters of Kilburn, took strident and emotive issue with Copeland’s argument, with one of them even claiming that Turing had contributed nothing to the development of computing. I repeat: this took place in Manchester 50 years after Turing’s death! Clearly there were people who did not like Turing, or in some way had been offended by him, and who were still extremely upset about it half a century later. They were still trying to belittle his contribution and his practical skills, despite the factual evidence to the contrary.
I applaud Gordon Brown’s courage in officially apologizing to Alan Turing, an apology which at least ensures the historical record is set straight for what our modern society owes this man.
POSTSCRIPT #1 (2009-10-01): The year 2012 will be a centenary year of celebration of Alan Turing.
POSTSCRIPT #2 (2011-11-18): It should also be noted, concerning Mr Brown’s statement, that Turing died from eating an apple laced with cyanide. He was apparently in the habit of eating an apple each day. These two facts are not, by themselves, sufficient evidence to support a claim that he took his own life.
POSTSCRIPT #3 (2013-02-15): I am not the only person to have questioned the coroner’s official verdict that Turing committed suicide. The BBC reports that Jack Copeland notes that the police never actually tested the apple found beside Turing’s body for traces of cyanide, so it is quite possible it had no traces. The possibility remains that he died from an accidental inhalation of cyanide or that he was deliberately poisoned. Given the evidence, the only rational verdict is an open one.
Thinkers of renown
The recent death of mathematician Jim Wiegold (1934-2009), whom I once knew, has led me to ponder the nature of intellectual influence. Written matter – initially, hand-copied books, then printed books, and now the Web – has been the main conduit of influence. For those of us with a formal education, lectures and tutorials are another means of influence, more direct than written materials. Yet despite these broadcast methods, we still seek out individual contact with others. Speaking for myself, it is almost never the knowledge or facts of others, per se, that I have sought or seek in making personal contact, but rather their various different ways of looking at the world. In mathematical terminology, the ideas that have influenced me have not been the solutions that certain people have for particular problems, but rather the methods and perspectives they use for approaching and tackling problems, even when these methods are not always successful.
To express my gratitude, I thought I would list some of the people whose ideas have influenced me, either directly through their lectures, or indirectly through their books and other writings. In the second category, I have not included those whose ideas have come to me mediated through the books or lectures of others, which therefore excludes many mathematicians whose work has influenced me (in particular: Newton, Leibniz, Cauchy, Weierstrauss, Cantor, Frege, Poincare, Pieri, Hilbert, Lebesque, Kolmogorov, and Godel). I have also not included the many writers of poetry, fiction, history and biography whose work has had great impact on me. These two categories also exclude people whose intellectual influence has been manifest in non-verbal forms, such as through visual arts or music, or via working together, since those categories need posts of their own.
Teachers & lecturers I have had who have influenced my thinking include: Leo Birsen (1902-1992), Sr. Claver Butler RSM (ca. 1930-2009), Burgess Cameron (1922-2020), Sr. Clare Castle RSM (ca. 1920- ca. 2000), John Coates (1945-2022), Dot Crowe, James Cutt, Bro. Clive Davis FMS, Tom Donaldson (1945-2006), Gary Dunbier, Sol Encel (1925-2010), Felix Fabryczny de Leiris, Claudio Forcada, Richard Gill (1941-2018), Myrtle Hanley (1909-1984), Sr. Jennifer Hartley RSM, Chip Heathcote (1931-2016), Hope Hewitt (1915-2011), Alec Hope (1907-2000), John Hutchinson, Marg Keetles, Joe Lynch, Robert Marks, John McBurney (1932-1998), David Midgley, Lindsay Morley, Leopoldo Mugnai, Terry O’Neill, Jim Penberthy* (1917-1999), Malcolm Rennie (1940-1980), John Roberts, Gisela Soares, Brian Stacey (1946-1996), James Taylor, Frank Torpie (1934-1989), Neil Trudinger, David Urquhart-Jones, Frederick Wedd (1890-1972), Gary Whale (1943-2019), Ted Wheelwright (1921-2007), John Woods and Alkiviadis Zalavras.
People whose writings have influenced my thinking include: John Baez, Ole Barndorff-Nielsen (1935-2022), Charlotte Joko Beck (1917-2011), Johan van Bentham, Mark Evan Bonds, John Cage (1912-1992), Albert Camus (1913-1960), Nikolai Chentsov (1930-1992), John Miller Chernoff, Stewart Copeland, Sam Eilenberg (1913-1998), Paul Feyerabend (1924-1994), George Fowler (1929-2000), Kyle Gann, Alfred Gell (1945-1997), Herb Gintis, Jurgen Habermas, Charles Hamblin (1922-1985), Vaclav Havel (1936-2011), Lafcadio Hearn (1850-1904), Jaakko Hintikka (1929-2015), Eric von Hippel, Wilfrid Hodges, Christmas Humphreys (1901-1983), Jon Kabat-Zinn, Herman Kahn (1922-1983), John Maynard Keynes (1883-1946), Andrey Kolmogorov (1903-1987), Paul Krugman, Imre Lakatos (1922-1974), Trevor Leggett (1914-2000), George Leonard (1923-2010), Brad de Long, Donald MacKenzie, Saunders Mac Lane (1909-2005), Karl Marx (1818-1883), Grant McCracken, Henry Mintzberg, Philip Mirowski, Michel de Montaigne (1533-1592), Michael Porter, Charles Reich (1928-2019), Jean-Francois Revel (1924-2006), Daniel Rose, Bertrand Russell (1872-1970), Pierre Ryckmans (aka Simon Leys) (1935-2014), Oliver Sacks (1933-2015), Gunther Schuller (1925-2015), George Shackle (1903-1992), Cosma Shalizi, Rupert Sheldrake, Raymond Smullyan (1919-2017), Rory Stewart, Anne Sweeney (d. 2007), Nassim Taleb, Henry David Thoreau (1817-1862), Stephen Toulmin (1922-2009), Scott Turner, Roy Weintraub, Geoffrey Vickers VC (1894-1982), and Richard Wilson.
FOOTNOTES:
* Which makes me a grand-pupil of Nadia Boulanger (1887-1979).
** Of course, this being the World-Wide-Web, I need to explicitly say that nothing in what I have written here should be taken to mean that I agree with anything in particular which any of the people mentioned here have said or written.
A more complete list of teachers is here.
Newton and scientific publication
While on the subject of Isaac Newton, here are several statements by historian Scott Mandelbrote on Newton’s attitude to the public dissemination of his work. The more we know of Newton, the less we should consider him a scientist in the modern meaning of the word.
His [theological investigation] was a voyage of personal discovery; even the Principia required Halley’s exertions as a midwife to bring them to light. Newton might share his religious opinions with other members of the remnant, as he did in his letters to Locke, but he worried about the consequences of their wider dissemination: ‘I was of opinion my papers had lain still & am sorry to heare there is news about them. Let me entreat you to stop their translation & impression so soon as you can for I designe to suppress them.’ Newton’s concern may have reflected fear of being discovered to hold unorthodox opinions, but it was also the product of religious motives. Not everyone could be expected to comprehend ‘strong meat’, which was intended for personal consumption, and which might be wasted on others.” (p.299)
His [Newton’s] theology pervaded his alchemy, in his analysis of the Emerald Tablets of Hermes Trismegistus, and in turn his alchemy suggested to him how matter might be understood physically. A true understanding of the uses of language enabled Newton to introduce astronomical calculation into his chronological writings, and to complete his mathematical arguments with theological references:
[pagebreak]
. . . .
Mathematics was God’s language; the language of the prophets communicated God’s purposes and ‘times’ to men. Newton felt it was his duty to understand and to reconcile the two, to decipher the hieroglyphs which corrupted religion and learning had obscured. The problems of mathematics ended in the solutions of divine majesty, and mathematical language solved the theological problem of describing Newton’s Arian interpretation of the relations within the Trinity:
. . .
Newton’s natural philosophical and theological discoveries removed the obscurities from divine language, in the books of nature and of scripture. In the life of the true believer, the two could not be separated. But most had to be content with the milk for babes, because Newton’s own language was beyond them.” (pp. 300-301).
Reference:
Scott Mandelbrote [1993]: ‘A dute of the greatest moment’: Isaac Newton and the writing of biblical criticism. British Journal of the History of Science, 26: 281-302.
A salute to Thomas Harriott
Thomas Harriott (c. 1560-1621) was an English mathematician, navigator, explorer, linguist, writer, and astronomer. As was the case at that time, he worked in various branches of physics and chemistry, and he was probably the first modern European to learn a native American language. (As far as I have been able to discover, this language was Pamlico (Carolinian Algonquian), a member of the Eastern Algonquian sub-family, now sadly extinct.) He was among those brave sailors and scientists who traversed the Atlantic, in at least one journey in 1585-1586, during the early days of the modern European settlement of North America. Because of his mathematical and navigational skills, he was employed variously by Sir Walter Raleigh and by Henry Percy, 9th Earl of Northumberland, both of whom were rumoured to have interests in the occult and in the hermetic sciences. Harriott was the first person to use a symbol to represent the less-than relationship (“<“), a feat which may seem trivial, until you realize this was not something that Babylonian, Egyptian, Greek, Islamic, Indian, or Chinese mathematicians ever did; none of these cultures were slouches, mathematically.
Yesterday, 26 July 2009, was the 400th anniversary of Harriott’s drawing of the moon using a telescope, the first such drawing known. In doing this, he beat Galileo Galilei by a year. The Observer newspaper yesterday honoured him with a brief editorial.
Interestingly, Harriott was born about the same year as the poet Robert Southwell, although I don’t know if they ever met. Southwell spent most of his teenage years and early adulthood abroad, and upon his return to England was either living in hiding or in prison. So a meeting between the two was probably unlikely. But they would have each known of each other.
Previous posts in this series are here. An index to posts about the Matherati is here.
Art as Argument #3: commutative diagrams in Category Theory
Following these posts on whether art could be understood as arguments, I turn attention to diagrams in pure mathematics. I know of only two areas of mathematics where diagrams are used frequently as arguments in proofs, rather than simply as illustrations of arguments or proofs expressed in algebraic symbols. One area is Euclidean Geometry, which most of us learn in school. The other is category theory (CT). It is interesting that one of the oldest and one of the youngest branches of pure mathematics should be the only ones using diagrams in this way. Perhaps the rise of CT is another signal of the decline of the three-centuries-long dominance of the written word over western culture.
First, here is an example of a typical commutative diagram from category theory:
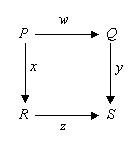
This particular diagram expresses an equivalence: that in traveling from P to S, it does not matter whether we travel via Q or we travel via R, the end-result will be the same. (Category theory makes this notion of “same-ness” or equivalence quite precise; indeed, in some sense CT is a formal theory about different notions of equivalence and their relationship to one another.) Thus, the diagram is making a claim about the (mathematical) world, a claim which may include its own proof: that executing function (or action) w followed by function y is the same as executing function x followed by function z.
Let us see what CT textbooks say to justify the subject’s use of diagrams. The standard reference on CT for mathematicians is the book by Saunders Mac Lane. An easier introduction is the book by Lawvere and Schanuel. Both of these simply start using diagrams as proofs without any justification for the practice, although they both formally define the diagrams concerned. In the book by Barr & Wells, we find:
When the target graph of a diagram is the underlying graph of a category some new possibilities arise, in particular the concept of commutative diagram, which is the categorist’s way of expressing equations.” (page 93)
Later in the same chapter they say:
This point of view provides a pictorial proof that the composite of two graph homomorphisms is a graph homomorphism. . . . . . The verification process just described is called “chasing the diagram”. Of course, one can verify the required fact by writing the equations (4.14) and (4.15) down, but these equations hide the source and target information given in Diagram (4.13) and thus provide a possibility of writing an impossible composite down. For many people, Diagram (4.13) is much easier to remember than equations (4.14) and (4.15). However, diagrams are more than informal aids; they are formally-defined mathematical objects just like automata and categories.“ (page 96)
Mac Lane says (p. 29) that the use of arrows as a graphical representation of functions was introduced by Hurewicz in about 1940, and that he also probably first used commutative diagrams. Like many practices in mathematics, one learns about the use of diagrams as proofs in CT in the classroom. Despite the textual (ie, non-diagrammatic) nature of most pure mathematical writing, parts of applied mathematics and theoretical physics (e.g. Feynman diagrams) use diagrams although pure mathematicians may question whether these disciplines are actually doing “proving”.
References:
Michael Barr and Charkes Wells [1999]: Category Theory for Computing Science. Montreal: Les Publications CRM, 3rd edition.
W. Hurewicz [1941]: On duality theorems. Bulletin of the American Mathematics Society, 47: 562-563.
F. W. Lawvere and S. H. Schanuel [1997]: Conceptual Mathematics: A First Introduction to Categories. Cambridge: CUP.
Saunders Mac Lane [1998]: Categories for the Working Mathematician. Berlin: Springer, 2nd edition.
The French Member of the English Language Committee of the IMO
The International Mathematics Olympiad is a famous international competition for mathematics students. This is an excerpt from the diary of the Chairman of the English Language Committee (ELC) of the 2005 IMO , Geoff Smith:
In the evening I prepare for the English language committee which I will chair next day. This means I slope off to my room early and try to cast the questions in perfect English myself, in order to have something to start with. The committee meets first thing in the morning. These days everyone is welcome in the ELC, including its most important member, the leader of France. We like to have simple sentences in IMO questions; ones which ideally can be translated almost word for word into as many languages as possible. French is rather special, and does not allow the rather free word order and grammatical latitude of English. Therefore the English language version has to be designed so that it can be easily translated into French. As each English sentence is suggested, we turn to FRA7, Claude Deschamps, to receive either a blessing (a shrug which indicates that all is well) or a sad shaking of the head which indicates that a particular piece of Anglo-Saxon thuggery simply cannot be expressed in French.”
Scenarios and possible worlds
Herman Kahn was the inventor of scenario analysis, and he first applied it to analysis of US military options in the Cold War with the USSR in the 1950s. I was struck when I read his books by the fact that scenarios were developed in the same decade as possible worlds semantics for logical systems or languages, and both at a time when most people felt there was a choice of only two or three over-arching political systems. (In contrast, from the fall of the Berlin Wall until the Global Financial Crisis, most people probably thought there was no such choice, western capitalism having prevailed over all alternative systems. Now, of course, nobody knows anything.)
I don’t think these simultaneous facts of scenarios and possible worlds were coincidences. Which leads me to a question that has long intrigued me: just who did develop possible worlds semantics? Although the idea dates at least to Leibniz, Saul Kripke is usually credited, and so these semantics are often called Kripke frames.
But there are other candidates:
- Richard Montague, logician and linguist, who published in 1960, but had presented his work at a conference at UCLA in 1955.
- Carew Meredith and Arthur Prior in 1956. According to Jack Copeland, these two logicians developed the first possible worlds semantics for propositional modal logic in a one-page note dated 1956. Meredith was a near contemporary of Frank Ramsey at Winchester and Trinity College, Cambridge.
- Charles L. Hamblin, whose London University PhD thesis submitted in October 1956 presents a possible worlds semantics for question-response interactions.
- Hugh Everett, who presented the first formal possible-worlds theory of quantum mechanics in physics, in his 1956 Princeton University PhD thesis.
- Jaako Hintikka, who developed a possible worlds semantics for logics of belief. Although published in 1962, I understand Hintikka’s work was completed as early as 1957.
- Stig Kanger, who published in 1957.
- A. Bayart, a Belgian logician, who published in 1958 and 1959.
As I said, it is exceedingly odd that all these works were published around the same time. In addition, both Everett and Kahn were at Princeton University in the 1950s, although I don’t know if they overlapped. Also, Kahn had studied physics, so may have been aware of recent developments in the subject.
References:
A. Bayart [1958]: Correction de la logique modale du permier et du second ordre S5. Logique et Analyse, 1 (1): 28-45.
A. Bayart [1959]: Quasi-adéquation de la logique modale du second ordre S5 et adéquation de la logique modale du premier ordre S5. Logique et Analyse, 2 (6-7): 99-121.
B. J. Copeland [1999]: Notes towards a history of possible worlds semantics. pp. 1-14 in: The GoldBlatt Variations: Eight Papers in honour of Rob. Uppsala Prints and Preprints in Philosophy, Number 1. Uppsala, Sweden: Department of Philosophy, Uppsala University.
H. Everett [1956]: The Theory of the Universal Wave Function. Princeton, NJ, USA: Princeton University Press. Reprinted as pp. 3-140 of: B. S. DeWitt and R. N. Graham [1973]: The Many Worlds Interpretation of Quantum Mechanics. Princeton, NJ, USA: Princeton University Press. The main results of Everett’s PhD were published in: H. Everett [1957]: “Relative State” formulation of Quantum Mechanics. Review of Modern Physics, 29 (3): 454-462.
Robert Goldblatt [2006]: Mathematical modal logic: a view of its evolution. D. M. Gabbay and J. Woods (Editors): Handbook of the History of Logic. Volume 7.
C. L. Hamblin [1957]: Language and the Theory of Information. London, UK: PhD Thesis, Logic and Scientific Method Programme, University of London. Submitted October 1956, awarded 1957.
J. Hintikka [1962]: Knowledge and Belief. Ithaca, NY, USA: Cornell University Press.
H. Kahn [1960]: On Thermonuclear War. Princeton, NJ, USA: Princeton University Press.
H. Kahn [1965]: On Escalation: Metaphors and Scenarios. Pall Mall Press.
S. Kanger [1957]: Provability in Logic. Stockholm Studies in Philosophy. Stockholm, Sweden: Almqvist and Wiksell.
S. Kripke [1959]: A completeness proof in modal logic. Journal of Symbolic Logic, 24: 1-14.
S. Kripke [1963]: Semantical analysis of modal logic I: normal propositional calculus. Zeitschrift fur mathematische Logic und Grundlagen der Mathematik, 9: 67-96.
How environment shapes cosmology
Further to the post below about the relationship between language and thought, a friend has just remarked to me that the absolute (East-West-North-South) spatial reference system in the language of the Kuuk Thaayorre is in fact a relative system, relative to the magnetic poles or (since they are unlikely to have known about the poles) relative to the movements of the sun. Accordingly, such a language would have been unlikely to have developed in parts of the world with continuous cloud cover. Which observation brought to mind a famous article by French mathematician and physicist Henri Poincare, where he considered what type of mathematical physics humans may have developed if the earth had been always covered in cloud: no theory aiming to predict the return of meteors, no models of planetary motion, not much study of ellipses and related number theory, and perhaps a theory of gravitation long delayed. (Thanks: DW).
The mathematics of jellyfish leaves much to be desired
A reader of Normblog presents a (standard) constructive argument for the counting numbers and then the infinite cardinals:
I happen to be friends with a jellyfish, called Jelly von Neumann. I asked Jelly about what Professor Atiyah said and she replied as follows…
‘Even if one has never seen any fish, crabs or the like, one may proceed as follows. First consider the empty set, { }, the set which has no elements whatsoever. Call that 0. Next, having got 0, consider the set {0}, whose only element is 0. Call that 1. Next consider the set {0, 1}, whose elements are exactly 0 and 1. Call that 2. Next consider the set {0, 1, 2}. Call that 3.
‘And so on. This gives you the infinite sequence 0, 1, 2, 3,… (One can prove that this sequence is infinite, since the operation involved is injective and never maps anything to 0.) You may even consider the whole infinite set, {0, 1, 2, 3,…}. Call this set omega. And you can go further. For consider the set {omega}. Call this omega + 1. Then consider {omega, omega + 1}, and call this omega + 2. Keep going. You get to omega + omega, and then omega + omega + omega. And so on. Eventually omega squared. Then omega cubed. And so on. Then omega to the power omega. And then (omega to the power omega) to the power omega. And then keep going. Eventually, you get to epsilon-zero. It gets a bit complicated after that. The point is that you can do mathematics just by virtue of thinking. Of course, I am a rather special jellyfish in that regard.’
Let us look carefully at the first few lines. Before we have defined or constructed a single number, we are expected to have available a notion of a set and a notion of an element of a set.
First consider the empty set, { }, the set which has no elements whatsoever.
This is very odd – we are people who apparently know some set theory, but we cannot yet count (since we have not yet constructed the counting numbers). And not just any set, but a set with no elements. So maybe we can count! How else can we tell that there are no elements in the empty set? Perhaps we can only count zero objects. And, moreover, this set is called “the empty set”, so presumably we know that there is only one of them. There’s some pretty advanced set theory right there, in that casual statement of uniqueness, I would say. (The claim of uniqueness, however, is not required for Jelly’s construction.)
Putting aside the question whether it is possible in principle for anyone, even those us with access to counting numbers, to count zero objects (arguably, counting is by definition an activity which requires the presence of at least one object to occur), let us continue with Jelly’s argument:
Call that 0.
So we can label objects.
Next, having got 0,
Wait a goddam minute, buster! We just labeled an object “{ }” with the label “0“. That is something different from getting or having anything. And surely, in order to label an object “{ }” with a label “0“, we must in some fundamental sense already had had the label “0“. If we did not already have it, how else could we use it to label an object? Jelly is using some pretty sleazy slight-of-hand here to slip from assigning a label that looks like a counting number to having the counting number itself, ready and able to be used for counting. If the label we had used was (say) the greek letter alpha, then Jelly’s argument would proceed in exactly the same way as before, but we would not end the argument having defined the counting numbers.
Ignoring these problems, let us proceed:
consider the set {0}, whose only element is 0.
So now “0″ is an object, available for use as the element of a set. And we not only know some set theory, we ALSO know how to construct sets! Just how do we do this? Do we pick the object (or the label?) called “0″ and put it inside some curly braces? How do we know when to start and stop picking objects? For some reason we picked just one object. Do we know how to count already? At the next step we construct a set with two objects:
Next consider the set {0, 1}, whose elements are exactly 0 and 1. Call that 2.
From what collection of objects (or labels?) did we select the one called “0″ , or (respectively) the ones called “0″ and “1″? We seem not only able to construct sets and to count objects, but we also know how to select particular objects (not just any old objects, but particular ones) from some undefined collection of objects. Quite some skills we have here, we people who don’t yet know how to count. And is the object that is here called “0” a different object with the same label as the one called “0” just three sentences before? If they are different, how many of these different objects with the same label do we have? And how can we tell them apart? And, if they are not different, we must be re-using the same object called “0”. Can we do this? When last handled by us (two sentences before), the object called “0” was sitting inside the set {0}. Can we just up and take it out and plonk it down inside the set {0,1}? There are lots of deep questions here, questions whose possibly-different answers motivate entire branches of pure mathematics (e.g., linear logic, which deals with formal logics where we have available only a fixed and finite number of each mathematical symbol), which our jellyfish-cum-mathematician is glossing over or ignoring.
After a few rounds of this, Jelly hits us with:
And so on. This gives you the infinite sequence 0, 1, 2, 3,…
Well, no, actually. We never get an infinite sequence, since we, in this universe, can only ever complete a finite number of such steps in our lifetimes. This is true even if all humans who ever lived, who are living, and who ever will live were to add their tuppence-worth of steps to the argument. It’s hard to have confidence in a jellyfish claiming to construct a collection of infinite cardinals who can’t seem to distinguish between a finite and an infinite sequence. At best (modulo the flaws identified above) we could get a finite, ever-growing sequence of counting numbers, a sequence that can be proven to exceed any pre-determined numerical threshold (thinking of these labels as real numbers for the moment), provided we allow sufficient time for the steps to be undertaken in the order described. A finite, ever-growing sequence is not ever an infinite sequence; at best, we might call it potentially-infinite.
I think Mr Jelly ought to forget the peano lessons and adopt a cat. And Norm, a Zimbabwean by birth, could perhaps remember how difficult it is to count objects in chiShona, with its ostentatious plenitude of noun-classes (21 according to Dale), and associated multitudes of counting words; urban Shona children nowadays usually count in English, even when they know little other English.
Reference:
D. Dale [1968]: Shona Companion. Mambo Press, Gweru, Zimbabwe. Second edition, 1972.