Following these posts on whether art could be understood as arguments, I turn attention to diagrams in pure mathematics. I know of only two areas of mathematics where diagrams are used frequently as arguments in proofs, rather than simply as illustrations of arguments or proofs expressed in algebraic symbols. One area is Euclidean Geometry, which most of us learn in school. The other is category theory (CT). It is interesting that one of the oldest and one of the youngest branches of pure mathematics should be the only ones using diagrams in this way. Perhaps the rise of CT is another signal of the decline of the three-centuries-long dominance of the written word over western culture.
First, here is an example of a typical commutative diagram from category theory:
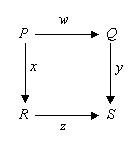
This particular diagram expresses an equivalence: that in traveling from P to S, it does not matter whether we travel via Q or we travel via R, the end-result will be the same. (Category theory makes this notion of “same-ness” or equivalence quite precise; indeed, in some sense CT is a formal theory about different notions of equivalence and their relationship to one another.) Thus, the diagram is making a claim about the (mathematical) world, a claim which may include its own proof: that executing function (or action) w followed by function y is the same as executing function x followed by function z.
Let us see what CT textbooks say to justify the subject’s use of diagrams. The standard reference on CT for mathematicians is the book by Saunders Mac Lane. An easier introduction is the book by Lawvere and Schanuel. Both of these simply start using diagrams as proofs without any justification for the practice, although they both formally define the diagrams concerned. In the book by Barr & Wells, we find:
When the target graph of a diagram is the underlying graph of a category some new possibilities arise, in particular the concept of commutative diagram, which is the categorist’s way of expressing equations.” (page 93)
Later in the same chapter they say:
This point of view provides a pictorial proof that the composite of two graph homomorphisms is a graph homomorphism. . . . . . The verification process just described is called “chasing the diagram”. Of course, one can verify the required fact by writing the equations (4.14) and (4.15) down, but these equations hide the source and target information given in Diagram (4.13) and thus provide a possibility of writing an impossible composite down. For many people, Diagram (4.13) is much easier to remember than equations (4.14) and (4.15). However, diagrams are more than informal aids; they are formally-defined mathematical objects just like automata and categories.“ (page 96)
Mac Lane says (p. 29) that the use of arrows as a graphical representation of functions was introduced by Hurewicz in about 1940, and that he also probably first used commutative diagrams. Like many practices in mathematics, one learns about the use of diagrams as proofs in CT in the classroom. Despite the textual (ie, non-diagrammatic) nature of most pure mathematical writing, parts of applied mathematics and theoretical physics (e.g. Feynman diagrams) use diagrams although pure mathematicians may question whether these disciplines are actually doing “proving”.
References:
Michael Barr and Charkes Wells [1999]: Category Theory for Computing Science. Montreal: Les Publications CRM, 3rd edition.
W. Hurewicz [1941]: On duality theorems. Bulletin of the American Mathematics Society, 47: 562-563.
F. W. Lawvere and S. H. Schanuel [1997]: Conceptual Mathematics: A First Introduction to Categories. Cambridge: CUP.
Saunders Mac Lane [1998]: Categories for the Working Mathematician. Berlin: Springer, 2nd edition.
0 Responses to “Art as Argument #3: commutative diagrams in Category Theory”